The Observer/Kalman System Identification Procedure Explained

Previously, we have had a look at the Eigensystem Realisation Algorithm (ERA) by Joung and Pappa. ( Citation: Juang & Pappa, 1985 Juang, J. & Pappa, R. (1985). An Eigensystem Realization Algorithm for Modal Parameter Identification and Model Reduction. Journal of Guidance Control and Dynamics, 8(5). https://doi.org/10.2514/3.20031 ) This algorithm allows us to find the parameters for a linear, time-invariant (LTI) system in discrete-time from measurements of the impulse response.

What, however, do we do when we don’t have measurements of the impulse response? We might not want to hit our system too hard, or have measurements with non-trivial inputs. Maybe we cannot wait for our system to return to a zero state before applying the impulse.

Again, Professor Steve Brunton came to the rescue with [two][https://youtu.be/TsdBeI6CKUM] [videos][https://youtu.be/lE8H0Z8-Ez8] on the Observer/Kalman System Identification procedure (or OKID for short) in his series on data-driven control.

Unfortunately, Prof. Brunton skips over the details and only gives a very short overview. Yet, I always try to understand the details of the methods I apply – if not for being able to assess when they may be used, then to learn about the principles being applied.

So I had a look into the papers by a group around Jer-Nan Juang, Minh Phan, Lucas G. Horta and Richard W. Longman, in which the OKID was introduced ( Citation: Juang, Phan & al., 1991 Juang, J., Phan, M., Horta, L. & Longman, R. (1991). Identification of Observer/Kalman Filter Markov Parameters: Theory and Experiments  (104069).  NASA Langley Research Center : Hampton, Virginia 23665. https://doi.org/10.2514/6.1991-2735 ) ( Citation: Phan, Juang & al., 1992 Phan, M., Juang, J. & Longman, R. (1992). Identification of Linear Multivariable Systems by Identification of Observers with Assigned Real Eigenvalues. Journal of the Astronautical Sciences, 40(2). 261–279. https://doi.org/https://doi.org/10.2514/6.1991-949 ) ( Citation: Phan, Horta & al., 1993 Phan, M., Horta, L., Juang, J. & Longman, R. (1993). Linear system identification via an asymptotically stable observer. Journal of Optimization Theory and Applications, 79(1). 59–86. https://doi.org/10.1007/BF00941887 ) . And again, there are some clever ideas in there that I found quite enlightening regarding handling the descriptions of dynamic systems:

• The basic approach of the OKID uses the fact that the response of an LTI to any input is related to the output by convolution of the impulse response.
• By reshaping the measurement data, a linear equation between said impulse response and the measurement data is established.
• This linear equation is solved using an ordinary least-squares approach.

The basic approach only works for asymptotically stable systems which approach zero state fast enough. However, there is a extension for non-stable or too slow systems: Instead of identifying the system itself, the OKID uses a modified system which is made asymptotically stable by a Luenberger observer ( Citation: Luenberger, 1964 Luenberger, D. (1964). Observing the State of a Linear System. IEEE Transactions on Military Electronics, MIL8. 74–80. https://doi.org/10.1109/TME.1964.4323124 ) , and then reconstructs the impulse response of the original system from the modified system.

Finally, this observer extension also leads to the “Kalman” part in the name for this procedure: The observer that is identified “on the go” this way turns out to be an optimal Kalman filter ( Citation: Kalman, 1960 Kalman, R. (1960). A New Approach to Linear Filtering and Prediction Problems. Transactions of the ASME - Journal of Basic Engineering, 82. 35–45. https://doi.org/10.1115/1.3662552 ) given the amount of noise seen on the measurements.

So, all in all, the whole approach is quite ingenious. However, it’s not as complicated as Professor Brunton makes it sound, and we’ll briefly go over it and its basic ideas in this article.

Review: Impulse Response

As for the ERA, we are dealing with discrete-time LTI systems. But different from previously, we’ll directly consider a Multiple Input, Multiple Output (MIMO) system.

The dynamics of this system shall be defined by the following recurrence equation:

Note that this time we also consider the case where the output is directly influenced by the output via the matrix [latex]\mathbf{D}[/latex]. Now, let’s assume that we have an input sequence [latex]\mathbf{u}_k[/latex] and observe the system starting at time step [latex]k_0[/latex]. We can determine the state [latex]\mathbf{x}_{k_0+r}[/latex] (with [latex]r \geq 0[/latex]) to be

\begin{equation} \mathbf{x}_{k_0+r} = \mathbf{A}^r \mathbf{x}_{k_0} + \sum_{j=1}^r \mathbf{A}^{r-j} \mathbf{B} \mathbf{u}_{k_0+j-1} \end{equation}

This can be verified by complete induction. For the case [latex]r=0[/latex] we get [latex]\mathbf{x}_{k_0} = \mathbf{A}^0 \mathbf{x}_{k_0} = \mathbf{x}_{k_0}[/latex].

For [latex]r \geq 0[/latex] we get

\begin{align} \mathbf{x}_{k_0+r+1} &= \mathbf{A} \mathbf{x}_{k_0+r} + \mathbf{B} \mathbf{u}_{k_0+r} \\
&= \mathbf{A} \mathbf{A}^r \mathbf{x}_{k_0} + \mathbf{A} \sum_{j=1}^r \mathbf{A}^{r-j} \mathbf{B} \mathbf{u}_{k_0+j-1} + \mathbf{B} \mathbf{u}_{k_0+r} \\
&= \mathbf{A}^{r+1} \mathbf{x}_{k_0} + \sum_{j=1}^r \mathbf{A}^{r+1-j} \mathbf{B} \mathbf{u}_{k_0+j-1} + \mathbf{B} \mathbf{u}_{k_0+r} \\
&= \mathbf{A}^{r+1} \mathbf{x}_{k_0} + \sum_{j=1}^{r+1} \mathbf{A}^{r+1-j} \mathbf{B} \mathbf{u}_{k_0+j-1} \end{align}

By extension, we can give the following expression for the output [latex]\mathbf{y}_{k_0+r}[/latex]:

\begin{align} \label{eq:markov-output} \mathbf{y}_{k_0+r} &= \mathbf{C} \mathbf{A}^r \mathbf{x}_{k_0} + \sum_{j=1}^r \mathbf{C} \mathbf{A}^{r-j} \mathbf{B} \mathbf{u}_{k_0+j-1} + \mathbf{D} \mathbf{u}_{k_0} \
&= \mathbf{C} \mathbf{A}^r \mathbf{x}_{k_0} + \underbrace{ \begin{bmatrix} \mathbf{C} \mathbf{A}^{r-1} \mathbf{B} & \cdots & \mathbf{C} \mathbf{B} & \mathbf{D} \end{bmatrix}}_{=:\mathbf{M}_r} \bar{\mathbf{u}}^{\left(r\right)}_{k_0} \end{align}

Here, we define the column vector [latex]\bar{\mathbf{u}}^{\left(r\right)}_{k_0}[/latex] by stacking the inputs at time steps [latex]k_0,\ldots,k_0+r[/latex] above each other:

\begin{equation} \bar{\mathbf{u}}^{\left(r\right)}_{k_0} = \begin{bmatrix} \mathbf{u}_{k_0} \\
\vdots \\
\mathbf{u}_{k_0+r} \end{bmatrix} \end{equation}

The matrix [latex]\mathbf{M}_r[/latex] gives us the so-called Markov-Parameters of length [latex]r[/latex], and when reversed, gives the impulse response of the system. If we had these Markov-Parameters, we could extract the system matrices with the help of the Eigensystem Realisation Algorithm (ERA).

Handling Asymptotically Stable Systems

For an asymptotically stable system, the term [latex]\mathbf{A}^r[/latex] approaches zero for increasing values of [latex]r[/latex]. Thus, for some sufficiently large [latex]p[/latex] we may assume that [latex]\mathbf{A}^p \approx \mathbf{0}[/latex].

This helps us in simplifying Equation \ref{eq:markov-output}

\begin{align} \label{eq:markov-output-stable} \mathbf{y}_{k_0+p} &= \mathbf{C} \underbrace{ \mathbf{A}^p}_{ \approx \mathbf{0}} \mathbf{x}_{k_0} + \mathbf{M}_p \bar{\mathbf{u}}^{\left(p\right)}_{k_0} \\
&\approx \mathbf{M}_p \bar{\mathbf{u}}^{\left(p\right)}_{k_0} \end{align}

Now, we can aggregate this into a larger equation:

\begin{equation} \begin{bmatrix} \mathbf{y}_{k_0+p} & \mathbf{y}_{k_0+p+1} & \cdots & \mathbf{y}_{k_0+n-1} \end{bmatrix} \\
\approx \\
\mathbf{M}_p \begin{bmatrix} \bar{\mathbf{u}}^{\left(p\right)}_{k_0} & \bar{\mathbf{u}}^{\left(p\right)}_{k_0+1} & \cdots & \bar{\mathbf{u}}^{\left(p\right)}_{k_0+n-p} \end{bmatrix} \end{equation}

With [latex]n[/latex] measurements (ideally, we have [latex]n \gg p[/latex]) we can thus find [latex]\mathbf{M}[/latex] by solving the equation above. Usually, this will be done using an ordinary least-squarey approach.

Handling Insufficient Stability

In the previous section, we assumed that the system we measure is asymptotically stable and is sufficiently damped so that we can have our measurement count [latex]n[/latex] sufficiently large relative to the length of our impulse response [latex]p[/latex]. So how do we handle systems where this is not the case?

Stabilisation Using a Luenberger Observer

The idea presented by Juang, Phan, Horta and Longman is quite simple: To arbitrarily choose the eigenvalues of the observed system, they construct a Luenberger observer. In general application, such an observer aims to reconstruct the internal state of a system from knowledge about the internal dynamics, about the inputs to the system and the measurements obtained from the system. It has the following structure:

\begin{align} \label{eq:observer-state} \hat{\mathbf{x}}_{k+1} &= \mathbf{A} \hat{\mathbf{x}}_k + \mathbf{B} \mathbf{u}_k - \mathbf{K} \left(\mathbf{y}_k-\hat{\mathbf{y}}_k\right) \\
\hat{\mathbf{y}}_k &= \mathbf{C} \hat{\mathbf{x}}_k + \mathbf{D} \mathbf{u}_k \end{align}

In this case, [latex]\hat{\mathbf{x}}_k[/latex] and [latex]\hat{\mathbf{y}}_k[/latex] represent the state of the observer, which according to the construction of the observer shall follow the state of the original system. The observer state is adjusted using the correction term [latex]-\mathbf{K} \left(\mathbf{y}_k-\hat{\mathbf{y}}_k\right)[/latex].

Usually, when constructing a Luenberger observer, we choose [latex]\mathbf{K}[/latex] given our knowledge about the original system in such a way that the observation error [latex]\mathbf{e}_k := \hat{\mathbf{x}}_k-\mathbf{x}_k[/latex] is asymptotically stable, i.e. approaches zero. The dynamics of this error are described as follows:

\begin{equation} \mathbf{e}_{k+1} = \left( \mathbf{A} + \mathbf{K} \mathbf{C} \right) \mathbf{e}_k \end{equation}

Given a completely observable system, we can select [latex]\mathbf{K}[/latex] in such a way that the eigenvalues of these error dynamics can be set arbitrarily. However, these eigenvalues also become the eigenvalues of the observer system, allowing us to arbitrarily stabilise it.

In our case, we want the observer state to be equal to the actual state, so we set [latex]\hat{\mathbf{x}}_k=\mathbf{x}_k[/latex], and arrive at the new state equations:

\begin{align} \label{eq:system-state-observer} \mathbf{x}_{k+1} &= \underbrace{ \left(\mathbf{A}+\mathbf{K} \mathbf{C}\right)}_{ =:\mathbf{\hat{A}}} \mathbf{x}_k + \underbrace{ \begin{bmatrix} \mathbf{B}+\mathbf{K} \mathbf{D} & -\mathbf{K} \end{bmatrix}}_{ =:\mathbf{\hat{B}}} \underbrace{ \begin{bmatrix} \mathbf{u}_k \\
\mathbf{y}_k \end{bmatrix}}_{ =:\mathbf{\hat{u}}} \\
\mathbf{y}_k &= \mathbf{C} \mathbf{x}_k + \underbrace{ \begin{bmatrix} \mathbf{D} & \mathbf{0} \end{bmatrix}}_{ =:\mathbf{\hat{D}}} \mathbf{\hat{u}} \end{align}

These equations describe the exact same system as in Equations \ref{eq:system-state} and \ref{eq:system-output}, but with the current output of the system [latex]\mathbf{y}_l[/latex] fed back into the system in such a way that the observed state always equals the actual system state. With this little trick, we have created a stable system to identify.

To find the Markov-Parameters [latex]\mathbf{\hat{M}}[/latex] of the new system, we simply apply the algorithm we used for sufficiently stable systems. This time, we use [latex]\mathbf{\hat{u}}_l[/latex] as input, which combines both the actual input and our measurement.

However, there’s one thing we need to be careful about: [latex]\mathbf{\hat{D}}[/latex] is not completely unconstrained in this problem. Indeed, its second part must be [latex]\mathbf{0}[/latex]. If we were to allow non-zero values there, the best fit would be [latex]\mathbf{\hat{D}} = \begin{bmatrix} \mathbf{0} & \mathbf{I} \end{bmatrix}[/latex], with all other system matrices being zero. This system would just forward the input [latex]\mathbf{y}_k[/latex] into its output. This would of course be a perfect fit – but it would not properly represent our system.

So instead, we have to find the best fit for

\begin{equation}
\begin{bmatrix} \mathbf{y}_{k_0+p} & \mathbf{y}_{k_0+p+1} & \cdots & \mathbf{y}_{k_0+n-1} \end{bmatrix} \
\approx \\
\mathbf{\tilde{M}}_p \begin{bmatrix} \bar{\mathbf{\hat{u}}}^{\left(p-1\right)}_{k_0} & \bar{\mathbf{\hat{u}}}^{\left(p-1\right)}_{k_0+1} & \cdots & \bar{\mathbf{\hat{u}}}^{\left(p\right)}_{k_0+n-p} \\
{\mathbf{u}}_{k_0+p} & {\mathbf{u}}_{k_0+p+1} & \cdots & {\mathbf{u}}_{k_0+n} \end{bmatrix} \end{equation}

Note how all rows consist of pairs of input and output, but the last row consists only of the input? This way, the identified system cannot feed through the measured output to its output, and instead the equation identifies the dynamics of the system we want to identify.

The result, however, does not yet represent the Markov-Parameters of our observer. Instead, it has the form

\begin{equation} \mathbf{\tilde{M}} = \begin{bmatrix} \mathbf{C} \mathbf{\hat{A}}^{r-1} \mathbf{\hat{B}} & \cdots & \mathbf{C} \mathbf{\hat{B}} & \mathbf{D} \end{bmatrix} \end{equation}

For recovery of the Markov-Parameters of the original system, this is quite inconsequential (we just have to be careful in the implementation). If we wanted to actually have the Markov-Parameters of the observer – which we might, as we will see when we look at the specific properties of that observer – then we would have to restructure the response as follows by appending an appropriately sized zero-matrix at the end:

\begin{equation} \mathbf{\hat{M}} = \begin{bmatrix} \mathbf{C} \mathbf{\hat{A}}^{r-1} \mathbf{\hat{B}} & \cdots & \mathbf{C} \mathbf{\hat{B}} & \mathbf{D} & \mathbf{0} \end{bmatrix} \end{equation}

Recovery of Original Markov-Parameters

But how do we get the Markov-Parameters of the original system? Again, Juang et al provide us with a little trick. Let’s first look at the structure of our stabilized Markov-Parameters:

\begin{align} \mathbf{\hat{M}} &= \begin{bmatrix} \mathbf{C} \mathbf{\hat{A}}^{r-1} \mathbf{\hat{B}} & \cdots & \mathbf{C} \mathbf{\hat{B}} & \mathbf{\hat{D}} \end{bmatrix} \\
&= \begin{bmatrix} \mathbf{\hat{M}}_{r} & \ldots & \mathbf{\hat{M}}_1 & \mathbf{\hat{M}}_{0} \end{bmatrix} \end{align}

with

\begin{align} \mathbf{\hat{M}}_{0} &= \begin{bmatrix} \mathbf{D} & \mathbf{0} \end{bmatrix} \\
\mathbf{\hat{M}}_r &= \mathbf{C} \left(\mathbf{A}+\mathbf{K} \mathbf{C}\right)^{r-1} \begin{bmatrix} \mathbf{B}+\mathbf{K} \mathbf{D} & -\mathbf{K} \end{bmatrix} \\
&=: \begin{bmatrix} \mathbf{\hat{M}}^{\left(1\right)}_r & \mathbf{\hat{M}}^{\left(2\right)}_r \end{bmatrix} \end{align}

Now, it is quite straightforward to extract [latex]\mathbf{D}[/latex] from [latex]\mathbf{\hat{M}}_0[/latex]. For the others, we find that

\begin{equation} \mathbf{\hat{M}}^{\left(1\right)}_r + \mathbf{\hat{M}}^{\left(2\right)}_r \mathbf{D} = \mathbf{C} \left(\mathbf{A}+\mathbf{K} \mathbf{C}\right)^{r-1} \mathbf{B} \end{equation}

For [latex]r=1[/latex], we can immediately recover [latex]\mathbf{M}_1[/latex]:

\begin{equation} \mathbf{M}_1 := \mathbf{C} \mathbf{B} = \mathbf{\hat{M}}^{\left(1\right)}_1 + \mathbf{\hat{M}}^{\left(2\right)}_1 \mathbf{D} \end{equation}

For [latex]r>1[/latex] we first expand the last element of the power:

\begin{align} \mathbf{\hat{M}}^{\left(1\right)}_r + \mathbf{\hat{M}}^{\left(2\right)}_r \mathbf{D} &= \mathbf{C} \left(\mathbf{A}+\mathbf{K} \mathbf{C}\right)^{r-1} \mathbf{B} \\
&= \mathbf{C} \left( \mathbf{A}+ \mathbf{K} \mathbf{C}\right)^{r-2} \mathbf{A} \mathbf{B} \nonumber\\
&+ \underbrace{ \mathbf{C} \left(\mathbf{A}+\mathbf{K} \mathbf{C}\right)^{r-2} \mathbf{K} }_{ =-\mathbf{\hat{M}}^{\left(2\right)}_{r-1}} \underbrace{ \mathbf{C} \mathbf{B} }_{=\mathbf{M}_1} \end{align}

Looking further, we can identify a pattern:

\begin{equation} \label{eq:markov-original-fwd} \mathbf{M}_r = \mathbf{\hat{M}}^{\left(1\right)}_r + \sum_{k=-1}^{r-1} \mathbf{\hat{M}}^{\left(2\right)}_{r-k-1} \mathbf{M}_k \end{equation}

The reader is encouraged to prove this identity by complete induction over [latex]\mathbf{r}[/latex]. Hint: First prove for [latex]s,t \geq 0[/latex] the following, more general identity:

With a few more steps Equation \ref{eq:markov-original-fwd} follows for [latex]t=0[/latex].

Thus, the Markov-Parameters [latex]\mathbf{M}_r:=\mathbf{C}\mathbf{A}^{r-1}\mathbf{B}[/latex] can be easily retrieved from Equation \ref{eq:markov-original-fwd}.

Why Kalman?

Now we know how the term “observer” got into the name. But how did “Kalman” end up there?

When we described the observer that we would use as model, we actually described a very specific observer, namely one that would immediately provide the same output as the actual system. The authors of the OKID paper ( Citation: Juang, Phan & al., 1991 Juang, J., Phan, M., Horta, L. & Longman, R. (1991). Identification of Observer/Kalman Filter Markov Parameters: Theory and Experiments  (104069).  NASA Langley Research Center : Hampton, Virginia 23665. https://doi.org/10.2514/6.1991-2735 ) use the term “deadbeat observer” for this. This is the fastest possible observer for a discrete time system. Any faster, and the observer would predict the output of the system, violating causality.

Indeed, later in the paper, the authors show that this deadbeat observer is identical with the Kalman filter one would find given the variance of noise seen in the measurement. A more detailed explanation of their proof might follow in a later article.

Thus, extracting not only the original Markov Parameters, but also the parameter [latex]\mathbf{K}[/latex] for the observer may be very beneficial if one wanted to design a Kalman filter for the system.

How do we get the system parameters for this Kalman filter? Well, we already have its Markov parameters, given by [latex]\mathbf{\hat{M}}[/latex], and can use the ERA on them. That gives us dynamics matrices for a Kalman filter.

Example

Let’s apply this method to our spring pendulum example from the ERA article. Remember: We had a horizontal spring pendulum with the following setup:

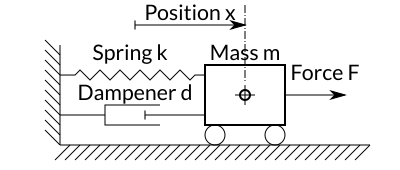
Different from the case with ERA, we now use an arbitrary input signal (which is the force [latex]F[/latex] applied to the mass), and determine the output signal. Again, we simulate the system and add noise to the output. The result is shown in the following figure.

The input is a pseudorandom binary sequence (PRBS). Such sequences can be generated, e.g., using the max_len_seq function from the SciPy signal processing library.

As we know from the ERA experiments, our pendulum is quite stable, so we can use the method for asymptotically stable systems. The result is shown in the following figure:

It seems that the estimate fits the actual impulse response (this time without noise) quite well. However, we’re in a dilemma:

• If we increase the length of our estimated impulse response, we reduce the amount of data we have available to counter all the noise, and thereby also the quality of our estimate.
• If we decrease the length of our estimated impulse response, we get a better estimate, but we have less data for our ERA procedure.

So we need to find a good compromise there by playing with the length of our estimated impulse response.

Conclusion

We have seen that the idea of the OKID procedure is not as involved as one might believe. The basis are three very simple ideas:

• The Markov Parameters determine the impulse response, and thereby define the input-output relationship – together with the initial state.
• For asymptotically stable systems, the influence of the initial state diminishes over time, eventually becoming so small that we can ignore it.
• Not sufficiently asymptotically stable systems can be made stable by considering a Luenberger observer in their place. The problem is then reduced to identifying the Markov Parameters for this observer, and retrieving the Markov Parameters for the original system from this intermediate result.
• The observer such identified actually is a Kalman filter for the system, given the noise seen in the measurement.

It seems useful to always use the observer-enhanced procedure by default. Even for sufficiently asymptotically stable systems the use of the observer would reduce [latex]p[/latex] and thus the amount of measurements required.

Now, finally, this opens up a lot of new possibilities for system identification: We can use the response to any set of inputs to determine the system model. This also allows us to identify a system that already is subject to control and where it would be impractical or impossible to remove that control. One simple example are flight-tests with an already controlled multicopter to improve the controller, but another would be to identify the progression of a disease without having to stop treatment (which of course would be unethical).

To take the design of a multicopter as an example, we could simply record in-flight data from sensors as well as the control inputs sent to our engines, and use that to improve our already existing model. We do not even have to provide specific inputs, but just a general recording of flight data will help, as long as it was rich enough.

Bibliography